Chapitres
- 01. Qu'est ce qu'un mouvement circulaire ? ⭕️
- 02. Le mouvement circulaire uniforme ?
- 03. Le mouvement circulaire non uniforme ?
- 04. Vitesse linéaire et vitesse angulaire ↪️
- 05. Expression mathématiques des vecteurs vitesse et accélération lors d'un mouvement circulaire ?
- 06. Cas particulier de la "force" centrifuge ?
Le cercle est le plus long chemin d'un point au même point.
Tom Stoppard
Depuis nos plus jeunes années, nous en traçons dans le sable, sur la nappe de table, dans les airs : le cercle est une forme plus que jamais universelle.
En géométrie, par convention, un cercle fait
degrés.
Mais au-delà de sa forme, tracer un cercle implique un mouvement, une trajectoire. Cela fait référence à différents éléments que l'on connaît au quotidien : une grande roue, une toupie, une roue de vélo, etc. Pourtant, un mouvement circulaire ne se résume pas qu'à quelque chose qui tourne, loin s'en faut !
Voici donc tout ce qu'il faut savoir sur les mouvements circulaires pour être incollable !
| Définition | Vecteur vitesse | Vecteur accélération | |
|---|---|---|---|
| Mouvement circulaire | Lorsqu'un point a une trajectoire de cercle (rotation, transition circulaire) | ||
| Mouvement circulaire uniforme | Si la vitesse reste constante au cours du temps. | Tangent au cercle de la trajectoire. | Constante en valeur, et dépend de la vitesse. |
| Mouvement circulaire non uniforme | Si la vitesse varie au cours du temps. | Tangent au cercle de la trajectoire mais sa norme varie au cours du temps. | Ne pointe plus vers le centre du cercle. |

Qu'est ce qu'un mouvement circulaire ? ⭕️

Un point possède un mouvement circulaire si sa trajectoire est un cercle ou une portion de cercle par rapport à un référentiel donné.
Il peut s'agir :
D'une rotation : tous les points de l'objet ont une trajectoire formant un cercle de rayons différents mais de même centre.
Par exemple, un satellite tournant autour de la terre ou le point de fixation de la nacelle d'une grande roue.
D'une translation circulaire : tous les points de l'objet ont une trajectoire formant un cercle de même rayon mais pas de même centre. C'est le cas de la nacelle de la grande roue. En effet, afin que la nacelle reste horizontale pour que les personnes puissent rester confortablement assises, la nacelle observe un mouvement translation circulaire (les centres des mouvements circulaires de la roue et de la nacelle sont différents).
@les_genies_des_sciences Caractériser un mouvement en physique #physique #bac #rectiligne #circulaire #curviligne ♬ son original - les génies des sciences
Au départ, les scientifiques ont commencé à étudier les mouvements circulaires en observant les trajectoire des planètes et de leurs satellites (même si l'on sait aujourd'hui que certaines de ces trajectoire forment des ellipses, plus que des cercles).

Puis, pour réaliser les premières machines sophistiquées, il a été nécessaire de prévoir le mouvement des composants la constituant.
Désormais, des logiciels sont capables d'effectuer des simulations identiques à la réalité.
Leur programmation a nécessité la connaissance des équations des trajectoires, notamment des mouvements circulaires (même si aujourd'hui les mouvements les plus complexes sont étudiés aux moyens de capteurs).
Il existe deux grands types de mouvements circulaires à connaître : le mouvement circulaire uniforme, et le mouvement circulaire non uniforme.
Le mouvement circulaire uniforme ?
Un mouvement circulaire est dit uniforme si la vitesse reste constante au cours du temps.
Par exemple, une épine dans la roue d'une voiture ayant son régulateur de vitesse à 130 km/h observe un mouvement circulaire uniforme par rapport à la route.

Le vecteur vitesse ?
En mathématiques, un vecteur pourrait être résumé par un segment qui indique une direction, un sens, mais aussi une longueur.
Pour comprendre ce qu'est le vecteur vitesse, il suffit d'imaginer un schéma avec deux points :
- O qui représente le centre du cercle,
- M qui représente le point en mouvement.
Le vecteur vitesse d'un mouvement circulaire est tangent au cercle de la trajectoire, donc perpendiculaire au rayon OM durant tout le mouvement.
Le mouvement étant uniforme, le vecteur vitesse est constant en norme.
Cependant contrairement à un mouvement rectiligne uniforme (celui de la voiture par rapport à la route par exemple), il n'est pas constant en direction puisqu'il est tangent au cercle de la trajectoire. en chaque point du mouvement.
Le vecteur accélération ?
Sur le même principe que le vecteur vitesse, le vecteur accélération est un outil mathématique utile pour comprendre les mouvements circulaires.
Contrairement à un mouvement rectiligne uniforme, la dérivée du vecteur vitesse n'est pas nulle, puisque sa direction change (mais pas sa norme). Par conséquent, l'accélération est elle-même non nulle.
Le vecteur accélération pointe en permanence vers le centre du cercle et possède une valeur égale à :

v est la vitesse (m.s-1)
R est le rayon du cercle de la trajectoire (m)
a est l'accélération (m.s-2)
L'accélération est donc constante en valeur et dépend de la vitesse ainsi que du rayon de la trajectoire.

L'accélération est dite centripète. C'est cette accélération qui permet le maintien de la trajectoire de l'objet.
Le mouvement circulaire non uniforme ?
Un mouvement circulaire est dit non uniforme si la vitesse varie au cours du temps.
C'est le cas de la même épine plantée dans le pneu de la voiture au moment de son entrée sur l'autoroute à 90 km/h pendant son accélération jusqu'à 130 km/h avant de mettre le régulateur (ou lors d'un coup de frein).

Le vecteur vitesse ?
Le vecteur vitesse garde les caractéristiques qu'il possède pour un mouvement circulaire uniforme : il est tangent au cercle de la trajectoire mais sa norme varie au cours du temps.
Le vecteur accélération ↔️
Dans ce cas, les caractéristiques du vecteur accélération sont différentes de celles appliquées lors d'un mouvement circulaire uniforme. Celui-ci ne pointe plus vers le centre du cercle.
Le vecteur accélération peut être alors défini à l'aide d'une composante dite normale, pointant vers le centre du cercle et d'une composante tangentielle, qui est colinéaire au vecteur vitesse :

L'accélération tangentielle ?
Cette composante du vecteur accélération est tangente au cercle de la trajectoire. Elle est donc colinéaire avec le vecteur vitesse.
Sa valeur peut être calculée à l'aide de la relation suivante :

L'accélération normale ?

Cette composante du vecteur accélération est normale (perpendiculaire) au cercle de la trajectoire.
Elle est donc orientée vers le centre du cercle, tout comme l'accélération du mouvement circulaire uniforme.
Sa valeur peut être calculée à l'aide de la relation suivante : 
La vitesse variant par définition au cours du temps, l'accélération normale varie donc elle aussi.

Vitesse linéaire et vitesse angulaire ↪️
Définitions ?
Lors d'un mouvement circulaire, la vitesse peut être exprimée de deux manières différentes :
La vitesse linéaire en m.s-1 qui est tangente au cercle de trajectoire, généralement notée v.
Son équation mathématique est la suivante :  (pour d la distance parcourue et t le temps de parcours).
(pour d la distance parcourue et t le temps de parcours).
La vitesse angulaire, qui exprime l'évolution de l'angle de rotation par rapport à sa valeur initiale en rad.s-1, généralement notée ω et l'angle θ.
Son équation mathématique est la suivante : 
Soit après intégration : 
Expression de la vitesse angulaire en fonction de la vitesse linéaire ?
La distance parcourue par un objet ayant une trajectoire circulaire peut-être définie selon le périmètre du cercle.
Ainsi, la vitesse, qui est par définition la distance parcourue en fonction du temps, peut s'exprimer de la manière suivante : 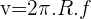 (avec R le rayon et f la fréquence de rotation).
(avec R le rayon et f la fréquence de rotation).
Exprimons maintenant également la vitesse angulaire en fonction de la fréquence de rotation : un tour complet, 2π radian est effectué en une période T (inverse de la fréquence).
La vitesse angulaire s'exprimant en radians par unité de temps, on peut donc écrire que :

On obtient donc :

Expression mathématiques des vecteurs vitesse et accélération lors d'un mouvement circulaire ?
Dans le plan ?
On se place dans le plan (x, y). Le mouvement circulaire est de rayon R et de centre O.
On peut alors calculer les coordonnées du point M effectuant un mouvement circulaire :
- En fonction du temps t et de l'angle θ :
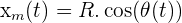 en abscisse et
en abscisse et 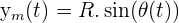 en ordonnée.
en ordonnée.
Le plus souvent, ce que nous connaissons (ou cherchons) plus que l'angle θ, c'est la vitesse angulaire.
Les coordonnées du vecteur vitesse étant la dérivée première et le vecteur accélération la dérivée seconde des coordonnées du point M (ou la dérivée première de la vitesse). En effet, nous avons vu plus haut que la vitesse angulaire n'est autre que la dérivée de l'angle et nous savons que l'accélération est la dérivée de la vitesse.

Dans le repère de Frenet ???
Les vecteurs associés aux accélérations normales et tangentielles peuvent également être exprimés à l'aide du repère de Frenet.
Également appelé repère de Serret-Frenet, le repère de Frenet est un outil d'étude des courbes. Il pourrait être résumé à la formation d'une tangente en un point d'une courbe, et de sa normale dans le plan. On le construit différemment selon la dimension (2D ou 3D).
Ce repère, qui peut être utilisé pour toutes les trajectoires curvilignes, a une origine mobile, correspondant au point en mouvement et possède deux vecteurs unitaires nommés N et T, représentés sur le schéma ci-dessous.
Dans le repère de Frenet, le vecteur accélération s'écrit :


Cas particulier de la "force" centrifuge ?
L'effet centrifuge, appelé à tort force centrifuge, est ressenti par l'objet en rotation. C'est ce qui explique que lors d'un mouvement circulaire, un corps à tendance à être éloigné du centre de rotation.
La force centrifuge dans un rond-point ?
Le passager d'une voiture dans un rond-point reste un très bon exemple. En effet, le point d'assise ne pouvant bouger, c'est le haut du corps que l'on sent entraîné vers l'extérieur du rond-point.
La force centrifuge d'une essoreuse à salade ?
C'est aussi cet effet là qu'utilise l'essoreuse à salade pour éjecter rapidement les gouttes d'eau présentes sur les feuilles.
Les gouttes sont projetées sur les parois par effet centrifuge et coulent au fond du récipient (c'est également le cas pour l'essorage lors d'un cycle de lavage en machine à laver).
@fabrikusworld LE ROTOR ! Venez tester la force centrifuge ?? #manège #manegeasensation #europarkviasplage #europark #parcdattraction #amusememtpark ♬ Banana (feat. Shaggy) [DJ FLe - Minisiren Remix] - Conkarah
Vecteur représentant la force centrifuge ✍️
La force centrifuge est représentée par un vecteur, qui comme le vecteur vitesse du mouvement circulaire est tangent au cercle de la trajectoire. Cependant son sens est opposé au vecteur vitesse du mouvement.
Expression mathématique de la force centrifuge ䷎
La valeur de la force centrifuge est proportionnelle à la masse de l'objet et à la vitesse de rotation de ce dernier.
Elle peut être exprimée en fonction de la vitesse angulaire ou linéaire :

- ω est la vitesse angulaire en (rad.s-1)
- v est la vitesse ( m.s-1)
- R est le rayon du cercle de la trajectoire (m)
- m la masse du corps en kg
La force centrifuge est exprimée en Newton (N).
À présent, vous savez tout sur les mouvements circulaires, et plus encore !























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Vraiment je vous remercie pour ce magnifique cours!
Bonjour cher professeur,j’ ai besoin de votre aide .
J’ ai besoin que vous m’ aidiez avec les documents maths, physique chimie et Svt en PDF ( cours et exercices) de la classe de 1ereD.
Merci de bien vouloir m’ aide cher professeur.
Bonjour, nous serions ravis de vous aider ! Rendez-vous sur la plateforme de Superprof, sélectionnez la rubrique “Découvrir nos Superprofs” en indiquant la matière désirée. Vous trouverez de nombreux professeurs près de chez vous. 🙂
Vous dite