Chapitres
🔬 Les ondes sinusoïdales, également appelées ondes sinusoïdales, jouent un rôle essentiel dans de nombreux domaines de la science, de la technologie et de la physique. Elles sont caractérisées par leur forme en sinus et sont décrites par des paramètres tels que l'amplitude, la fréquence, la phase et la période.
Découvrez-en plus sur ce type d'ondes et leurs applications concrètes 👏
Résumé sur le rôle d'une onde 👨🏫
🔉 Le son correspond a une vibration mécanique d'un fluide qui va alors se propager, grâce à la déformation élastique du fluide, en prenant la forme d'ondes longitudinales. Les Hommes, mais également beaucoup d'autres animaux, peuvent ressentir cette vibration grâce au sens que nous appelons l'ouïe.
👂 Les ondes sonores audibles sont caractérisées par des fréquences allant de 20 Hz à 20 kHz, ce qui correspond à des longueurs d'onde allant de 0,017 m à 17 m
Il existe trois types différents d’ondes :
- L'onde mécanique : Les ondes magnétiques nécessitent une matière qui se déforme afin de se propager. Ce matériau a la capacité recouvrer son état initial grâce aux forces de restauration qui inversent la déformation.
- L'onde électromagnétique : Les ondes électromagnétiques quant à elles n’ont pas besoin de support pour se déplacer : elles correspondent à des oscillation périodiques de champs électriques et magnétiques qui peuvent alors se déplacer dans le vide.
- L'onde gravitationnelle : Les ondes gravitationnelles n’ont plus de support pour se déplacer puisque ce sont les déformations de la géométrie de l’espace-temps qui se propagent.
Une onde mécanique progressive correspond a un phénomène de perturbation locale dans un milieu matériel. Ainsi, pour une onde mécanique, on ne peut observer de déplacement de matière mais un transport d’énergie.
Reconnaître une onde
🔎 Il existe différentes façons de mettre en valeur des ondes :
Onde à une dimension
- Corde vibrante
- Fibre optique
Deux dimensions
- Surface d’un plan d’eau
- Table d’harmonie d’un instrument de musique
Trois dimensions
- La propagation du son de l’orgue dans le volume intérieur d’une église
- Interférences lumineuses dans un espace
Phénomène de propagation d'une onde ⚛️
🍃 Lorsque l'onde se propage dans un milieu fluide compressible, il est possible d'observer une variation de pression qui va alors se propager sous la forme d'une onde. L'air nous entourant étant un milieu fluide compressible, il est alors possible de ressentir ces ondes sous la forme de son que l'on perçoit grâce aux tympans.
Cependant, pour qu'elle soit perceptible, il faut que la variation de pression, parce que son amplitude est faible par rapport à la pression atmosphérique, soit suffisamment rapide et répétée.
📣 Il est possible de considérer tout objet vibrant, tel qu'un instrument de musique ou encore un haut-parleur, comme étant une source sonore qui est donc, comme son nom l'indique, la source des vibration de l'air. La perturbation va alors se propager, même si les particules oscillent très peu (soit quelques micromètres autour d'une position stable), d'une façon analogue aux perturbations de l'eau lorsqu'une pierre y tombe : on peut observer des vagues qui s'éloignent peu à peu du point de perturbation bien que l'eau reste au même endroit.
🌊 En effet, l'eau ne se déplace que verticalement et ne suit pas les vagues (il est possible d'observer ce phénomène en plaçant un objet flottant près de la perturbation : il ne restera à la même position)
On peut alors dire que, dans les fluides, l'onde sonore correspond à une onde longitudinale. Ainsi, les particules observées vibrent de façon parallèle à la direction de déplacement de l'onde.
🫨 Une onde sonore peut également être transmise par un solide vibrant. En effet, la vibration va se propager au sein du solide comme dans les fluides : il y aura de faibles oscillation autour de la position d'équilibre des atomes constituant le solide. La conséquence est alors une contrainte du matériau qui, équivalente à la pression dans un fluide, est très difficile à mesurer. C'est donc la rigidité du matériau qui permettra la transmission des ondes de contraintes transversales.
Il peut être intéressant de noter que, la vitesse de propagation du son, également appelée célérité, varie selon différentes propriétés du milieu comme :
- La nature du milieu ;
- La température du milieu ;
- Et la pression du milieu.
⛽️ Ainsi, dans un gaz parfait, on peut obtenir la vitesse de propagation d'une onde sonore avec la relation suivante :
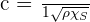
Avec :
- ρ correspondant à la masse volumique du gaz ;
- Et χS correspondant à la compressibilité isentropique du gaz.
Il est également possible d'observer une diminution de la vitesse du son lorsque :
- La densité du gaz augmente, on appelle cela l'effet d'inertie ;
- La compressibilité du gaz, c'est à dire sa capacité à changer de volume selon la pression qu'il subit, augmente.
Remarque : la vitesse du son
📚 Pour calculer la vitesse du son dont l'unité est, rappelons-le, le mètre par seconde, il est possible d'utiliser l'expression suivante :
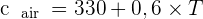avec T la température en degré Celsius
Mais il est possible d'être plus précis en utilisant les degrés Kelvin. On doit alors se servir de l'expression suivante :
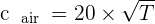
🎶 Notons que, de façon générale, la vitesse du son dans l'eau est de 1 500 m.s-1. Mais il existe de nombreux milieux où les ondes sonores peuvent se propager de façon encore plus rapide. On peut alors prendre l'exemple de l'acier au sein duquel les ondes se propage une vitesse comprise entre 5 600 et 5 900 m.s-1.
⚠️ Cependant, une onde sonore est incapable de se propager dans le vide puisqu'il faut nécessairement la présence de matière déformable pour que la vibration puisse se propager.
Les ondes progressives périodiques 📉
📝 Il est nécessaire de connaître quelques basiques :
- Une onde progressive correspond à la propagation dans l'espace et au cours du temps d'une perturbation.
- Une onde progressive est dite périodique si la perturbation qui la caractérise se répète à intervalles de temps réguliers, appelés périodes et notés T.
- Une onde ne peut être périodique que si sa source est elle-même périodique.
Comme tous les phénomènes périodiques, une telle onde est aussi caractérisée par sa fréquence f qui peut être calculée à partir de la relation suivante :
- avec T en seconde (s)
- f en Hertz ( Hz )
⏳ La fréquence caractérise la périodicité temporelle de l'onde.
La double périodicité des ondes mécaniques périodiques progressives
🤓 Prenons pour exemples deux points : M1 et M2.
- M1 et M2 vont reproduire le mouvement de la source. Ils vont vibrer à la même fréquence.
- Un point du milieu de propagation va se retrouver dans le même état vibratoire au bout d'une durée : T source.
- Les trois points M , M' et M'' se retrouvent au même instant dans le même état vibratoire, on dit qu'ils vibrent en phase. Ces points on les retrouve à intervalle d'espace régulier dans un milieu. On parle donc de périodicité spatiale.
Longueur d'onde : La distance séparant deux points consécutifs du milieu vibrant en phase est appelée longueur d'onde. On la note λ et s'exprime en mètre. Autrement dit, la longueur d'onde correspond à la distance parcourue par l'onde dans le milieu matériel pendant une période de vibrations de la source.
Onde stationnaire
📡 Une onde dite stationnaire correspond à la propagation simultanée et dans des sens opposés de plusieurs ondes de même fréquence et de même amplitude dans un même milieu. Ainsi, on observera une figure dont certains points sont fixes, appelés nœuds de pression, dans le temps. Il est alors possible d’observer une vibration stationnaire et d’intensité différente en chaque point observé au lieu de pouvoir observer une onde qui se propage.
Onde mécanique progressive
⚙️ Une onde mécanique progressive correspond a un phénomène de perturbation locale dans un milieu matériel. Ainsi, pour une onde mécanique, on ne peut observer de déplacement de matière mais un transport d’énergie.
Déplacement d’énergie
⚡️ L’onde, lorsqu’elle se propage, s’accompagne d’une modification temporaire des propriétés du milieu comme la position, la vitesse et la distance entre les particules constitutives du milieu modifié.
Ainsi, l’énergie, qu’elle soit potentielle ou cinétique, varie lorsque le signal est atteint. Notez tout de même que la variation d’énergie est temporaire et se déplace de proche en proche : elle ne dure que le temps de passage de l’onde.
Les ondes progressives périodiques sinusoïdales 📝
Une onde progressive est dite sinusoïdale si les variations de la perturbation se font en suivant la fonction mathématiques sinus.
On peut identifier ce type de fonction à partir du graphe comportant une alternance de "vagues" positives et négatives de mêmes amplitudes, tel qu'indiqué ci-dessous.
Exemple de représentation de la grandeur physique liée à une onde progressive périodique sinusoïdale
👍 Une onde progressive sinusoïdale possède, en plus d'une périodicité temporelle, une périodicité spatiale (répétition de la déformation). Si la périodicité temporelle est, nous l'avons vu, définie par la fréquence, la périodicité spatiale est, quant à elle définie, par la longueur d'onde.
La longueur d'onde d'une onde progressive périodique
📐 Une onde progressive périodique est également caractérisée par une longueur d'onde. Celle-ci peut être définie deux manières :
- Il s'agit de la distance qui sépare deux points en phase consécutifs.
- Il s'agit également de la distance sur laquelle se propage une perturbation pendant une durée correspondant à une période. Comme pour les ondes électromagnétiques la longueur d'onde se note avec la lettre grecque λ et peut être calculée avec les relations suivantes :
- avec λ en mètre (m)
- v (célérité de l'onde) en mètre par seconde (m.s-1)
- T en seconde (s)
- f en hertz (Hz)
Célérité d'une onde progressive sinusoïdale
🏃♂️ La célérité d'une onde progressive sinusoïdale est fonction des périodicités temporelle et spatiale. Elle correspond au temps nécessaire à un point pour parcourir la distance entre deux surfaces d'onde identiques (à l'amplitude maximale par exemple).
Il est préférable de parler de célérité plutôt que de vitesse, car il n'y a pas nécessairement de déplacement de matière dans le cas de l'onde progressive. La vitesse est plutôt utilisée dans le cas de déplacement d'un mobile par exemple.
La célérité d'une onde périodique sinusoïdale est constante dans le temps dans un milieu donné. Elle ne dépend pas de l'amplitude de l'onde. Par contre, elle est très dépendante du milieu de propagation.
🤸♂️ Prenons l'exemple du ruban de gymnastique rythmique et sportive, que l'on assimilera à une corde :
- Admettons que la gymnaste imprime un mouvement sinusoïdal, la célérité de propagation de la déformation dépendra du diamètre du ruban, de son élasticité et de sa densité donc du matériau qui le constitue
- Pour un même mouvement l'impression visuelle sera grandement changée.
Le tableau suivant résume les conséquences sur la célérité d'une onde (même perturbation initiale) suivant le type de ruban (corde) :
| Ruban | Ruban 1 | Ruban 2 | Ruban 3 | Ruban 4 | Ruban 5 |
|---|---|---|---|---|---|
| Rayon r | r | 2r | r | r | r |
| Densité d | d | d | d/2 | d | d/2 |
| Elasticité E | E | E | E | E/8 (8 fois plus élastique) | E/4 (4 fois plus élastique) |
| Célérité (m/s) | c | c/2 | 2c | c/4 | c |
Pour la gymnaste, le choix du matériau est primordial, car pour obtenir le même effet, elle devra imprimer un mouvement plus ou moins important et/ou rapide au départ suivant la nature du ruban.
🎀 Ainsi, l'on remarque que :
- Moins le ruban est dense, plus le mouvement se propage rapidement
- Par contre, plus le ruban est épais ou élastique moins le mouvement se propage rapidement
Ceci se comprend aisément, car d'une part, plus la corde est lourde plus il est difficile à déformer, et d'autre part, plus elle est élastique plus elle aura une déformation qui "absorbera" l'énergie d'oscillation apportée par la source de l'onde.
👉 À noter qu'en jouant sur plusieurs paramètres, il est possible d'obtenir une célérité identique avec une même impulsion initiale sur deux rubans de caractéristiques différentes.
Expression mathématique de l'onde sinusoïdale
🧑🏼🏫 Une onde périodique sinusoïdale, nous l'avons dit, suit une loi mathématique : la fonction sinus.
Cette propriété permet de pouvoir connaitre les caractéristiques de l'onde au cours du temps et en fonction de l'espace.
🤓 Si l'on étudie le mouvement sinusoïdale d'une onde monodimensionnelle dans un repère orthogonale (x ; y) de centre O, la position en ordonnée de chaque point en fonction du temps est donné par la relation mathématique suivante :
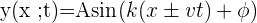
- avec A, l'amplitude de l'onde sinusoïdale en mètres notés m,
- k, le nombre d'onde, qui est une constante caractéristique de l'onde dépendant de sa longueur d'onde en radians par mètres notés rad/m,
- v, la célérité de l'onde en mètres par secondes noté m/s,
- t, le temps en secondes notés s,
- et ϕ, la constante de phase en radians notés rad. Elle correspond à la position de l'onde quand x et t sont nuls, soit au départ du mouvement. Si possible, dans un repère bien choisi, le centre du repère est placé au démarrage de l'onde et donc ϕ est nul.
Par convention :
- Si l'onde se déplace dans les sens des x croissants (vers la droite) alors la célérité de l'onde est positive et l'expression est la suivante :
- Si l'onde se déplace dans les sens des x décroissants (vers la gauche) alors la célérité de l'onde est négative et l'expression est la suivante :
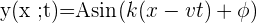
Le nombre d'ondes
📝 Le nombre d'onde est un paramètre mathématique servant à convertir la position x d'un point à sa valeur correspondante en radian (de la même manière que pour passer du sinus sur le cercle trigonométrique à l'abscisse sur un repère pour la fonction sinus) :
- avec k, le nombre d'onde en radians par mètres notés rad/m,
- 2π, la périodicité temporelle de l'onde, soit un cycle complet de la fonction sinus, en radians notés rad,
- et λ, la périodicité spatiale de l'onde en mètres notés m.
Le nombre d'onde est caractéristique de l'onde étudiée.
Déphasage entre deux ondes sinusoïdales progressives
Le déphasage initial correspond à la constante de phase ϕ. Graphiquement cela correspond au décalage du point de départ de la fonction sinus.
Deux ondes sinusoïdales peuvent être strictement identiques mais en décalage de phase. Elles seront caractérisées par la même fonction d'onde sinusoïdale à ϕ près.
🚨 Si deux ondes parcourent le même milieu simultanément, les amplitudes de deux ondes sonores de même nature se superposent, ainsi :
- Deux ondes identiques et de même nature non déphasées (ou avec un déphasage multiple de 2π) vont avoir une amplitude doublée car seront maximales au même moment.
- Deux ondes identiques et de même nature en opposition de phase (décalée d'un multiple impair de π) vont s'annuler car l'une sera maximale quand l'autre minimale. C'est ce principe qui est utilisé pour les casques anti-bruit avec réduction active.
La réaction de la lumière face à un nouveau milieu 💡
Indice d’un milieu transparent
🌦️ Un milieu transparent est caractérisé par son indice de réfraction. L'indice de réfraction d'un milieu transparent correspond au rapport entre la célérité d'une onde se propageant dans le vide et sa célérité dans le milieu considéré.
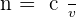
Avec :
- n correspondant à l'indice de réfraction du milieu transparent et qui est une grandeur sans unité ;
- c correspondant à la célérité de l'onde dans le vide. La célérité est égale à 3.108 m.s-1 ;
- Et v correspondant à la célérité de l'onde dans le milieu transparent qui s'exprime en m.s-1.
Un milieu est dit "dispersif" si la célérité d'une onde lumineuse monochromatique qui se propage dans ce milieu dépend de sa fréquence (donc de sa longueur d'onde dans le vide).
📚 L'indice de réfraction d'un milieu dispersif dépend donc de la fréquence de l'onde qui s'y propage.
- Dans un milieu transparent, la lumière se propage à la vitesse v=c/n.
- n est l’indice du milieu : grandeur sans dimension, supérieure à 1 et fonction de la longueur d’onde.
- Longueur d’onde dans un milieu d’indice n : λmilieu = λ/n.
- Quelques valeurs :
| Température (en °C) | Indice de réfraction de l'air |
|---|---|
| - 20 | 1,00031489 |
| - 10 | 1,000302844 |
| 0 | 1,000291647 |
| 10 | 1,000281196 |
| 20 | 1,000271373 |
La loi de Descartes sur la réfraction de la lumière
♣️ Cette loi lie les indices de réfraction (n1 et n2), l'angle d'incidence (i1) et l'angle de réfraction (i2). Elle s'exprime par la relation suivante :
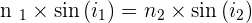
Définition : La réfraction de la lumière correspond au changement de direction du rayon lumineux lorsque celui-ci traverse une surface séparant deux milieux d'indices de réfraction différents.
En effet, la loi de Snell-Descartes de la réfraction exprime le changement de direction d'un faisceau lumineux lors de la traversée d'une paroi qui sépare deux milieux différents. Il faut d'abord savoir que chaque milieu est caractérisé par sa capacité à « ralentir » la lumière.
👉 On modélise cette caractéristique par son indice de réfraction n qui s'exprime sous la forme :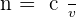
Où v est la vitesse de la lumière dans ce milieu et c est la vitesse de la lumière dans le vide (souvent arrondie à 3.108 m.s-1
Il est important de savoir que :
- Le rayon lumineux est dit incident avant d'avoir rencontré la surface réfractante (appelée dioptre), il est dit réfracté après avoir rencontré cette dernière.
- Le point de rencontre du rayon incident et du dioptre est appelé point d'incidence.
- Le plan contenant le rayon incident et la normale au dioptre, au point d'incidence est dit plan d'incidence.
- L'angle orienté i1 pris entre la normale au point d'incidence et le rayon incident est dit angle d'incidence.
- L'angle orienté i2 pris entre la normale au point d'incidence et le rayon réfracté est dit angle de réfraction.
- Les angles i1 et i2 sont positifs s’ils sont orientés dans le sens trigonométrique (sens inverse des aiguilles d'une montre), négatifs sinon.
On prend n1 l'indice de réfraction du milieu dans lequel se propage le rayon incident et n2 celui du milieu dans lequel se propage le rayon réfracté.
⚠️ Pour pouvoir énoncer la loi de la réfraction, il faut que le rayon réfracté, le rayon incident et la normale (au dioptre) soient dans un même plan qui est appelé le plan d'incidence et que le rayon incident et le rayon réfracté soient situés de part et d'autre de la normale.
Lorsque n1 > n2 (et respectivement n1 < n2) le rayon réfracté (et respectivement : incident) se rapproche plus rapidement du dioptre que le rayon incident (ou réfracté). Cependant, il existe un cas particulier où le rayon réfracté (ou incident) se retrouve mathématiquement sur le dioptre (sa limite) : il y a alors réflexion totale.
Bonus : comment caractériser une onde sonore ✅
Le décibel
Le décibel, en acoustique environnementale, permet d'indiquer le niveau de bruit. En effet, cette grandeur permet d'exprimer le rapport de puissance existant enter la pression acoustique et une valeur de référence qui a été choisie comme correspondant à un son imperceptible.
💥 D'une façon générale, le niveau sonore en champ libre, ce qui signifie sans obstacle sur le trajet de l'onde, est inversement proportionnel au carré de la distance, c'est-à-dire à la distance multipliée par elle-même.
La pression acoustique
La pression acoustique correspond à une grandeur physique qui stimule l'audition humaine. La plage de pression qui donne un niveau sonore perceptible par l'Homme est comprise entre un rapport de un et plusieurs millions.
🙉 Attention cependant, la percepteur du volume sonore est, de façon approximative, logarithmique. Cela signifie alors qu'une augmentation définie du volume correspondra à multiplier la pression par un facteur qui est identique. C'est pourquoi on ne convertit que très rarement la mesure du bruit, qui est de façon générale, correspondant à la pression acoustique en décibel.
L'intensité acoustique
📶 Afin de déterminer les chemins de propagation des sons dans un environnement, les études acoustiques utilisent fréquemment l'intensité acoustique. Cette grandeur correspond à la représentation de la puissance acoustique qui est transmise dans une direction définie. S'établissant généralement à partir d'un gradient de pression, on utilise logiquement un réseau de capteurs ou encore en ensemble de capteurs de vitesse acoustiques que l'on couple à un capteur de pression.
🚨 Attention toutefois aux confusions. En effet, parler d'une intensité acoustique n'induit pas toujours que l'on parle d'un niveau sonore. Il suffit pour démontrer cela de prendre l'exemple d'une onde stationnaire : son intensité est nulle alors que la pression acoustique ne l'est pas et l'on entend pourtant un son.
Une onde dite stationnaire correspond à la propagation simultanée et dans des sens opposés de plusieurs ondes de même fréquence et de même amplitude dans un même milieu. Ainsi, on observera une figure dont certains points sont fixes, appelés nœuds de pression, dans le temps. Il est alors possible d’observer une vibration stationnaire et d’intensité différente en chaque point observé au lieu de pouvoir observer une onde qui se propage.
La puissance acoustique
🎧 Afin de comparer deux sources de bruit, il est nécessaire d'utiliser la puissance acoustique qui s'exprime en dB SWL. Il est possible d'obtenir la valeur de cette grandeur en plaçant la source que l'on souhaite tester dans une chambre réverbérante afin que les sons soient mélangés dans toutes les directions. Mais il est également possible d'obtenir cette valeur en effectuant une série de mesures tout autour de la source sonore à tester.
Vous avez aimé cet article ? Notez-le !
Loading...
Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Lorsqu’on fixe le temps est-ce que on obtient un sinusoide d’espace ou de temps
Bonjour je trouve le cours très intéressant et complet mais j’ai une question. La périodicité correspond vraiment a quoi ?
Bonjour, à un entrecoupage !
Bonne journée !
Bonjour,
Merci pour ces explications bien claires.
Cependant,je ne comprends pas le schéma “Atténuation de l’intensité sonore avec la distance à l’émetteur” car sur le schéma, on voit que le niveau d’intensité sonore baisse de 80 à 77 puis à 74 dB soit une baisse de 3 dB lorsque la distance double alors que cela devrait baisser de 6 db?
Merci de votre réponse
Bonjour ! Êtes-vous bien sûr de parler du bon article ? Bonne journée !
Bonjour
Quel programme avez-vous utiliser pour observer ces différents spectres ?
Bonjour ! Pour observer ces spectres, on peut utiliser la méthode dite de la décomposition de la lumière, qui s’applique très bien ici.
Bonne journée !
Bonjour, j ai un calcul a faire or aucune valeur n’est mentionné : N(I) = 10log (I/Io) il est expliqué que Io est l’intensité de référence qui correspond a l’intensité la plus faible pour un son de f=1000Hz.
On me demande de calculer Io
Comment faire svp
Bonjour ! Nous vous expliquons comment calculer l’intensité dans une leçon dédiée : http://www.superprof.fr/ressources/scolaire/physique-chimie/terminale-s/ondes-periodiques/intensite-sonore.html#chapitre_calculer-intensite-sonore-a-partir-du-niveau-intensite
Bonne journée !